Skip to content

本文是按照我在图书馆随便翻来的一本书为指导展开的，感觉还行，就用了😋

大抵是本人拿来学学数据结构/算法的，也不知道学咋样😋

第1章：利用快速幂提高幂运算速率

1.1:基础快速幂算法

int quickpow(int n,int i){
    int ans = 1,res = n;
    while(i>0){
        if(i%2==1){
            ans*=res;
        }
        i/=2;
        res=res*res;
    }
    return ans;
}
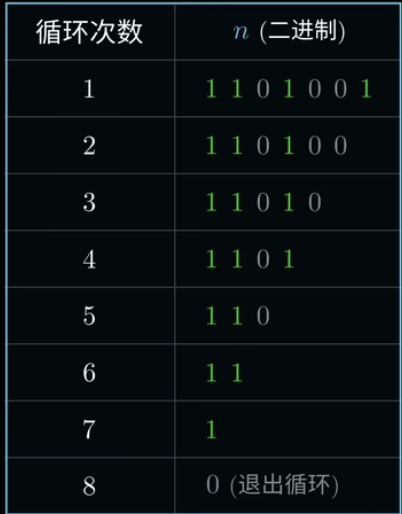看过一个视频，它解释这段代码的观点采取了二进制，笔者认为值得贴出来学习
Explain：这是计算 \(7^ {105}\)对指数的处理

因此，对源代码我们可以进行以下处理： 

int quickpow(int n,int i){
    int ans = 1,res = n;
    while(i>0){
        if(i % 1){//修改1
            ans*=res;
        }
        i = i >> 1;//修改2
        res=res*res;
    }
    return ans;
}
时间复杂度：O(\(\log_{2}{n}\))

查缺补漏：二进制

称它为二进制数是因为它只有0和1两个数字，用数学语言来说就是基数为2。依次类推，基数为3的是三进制计数、……、基数为10的就是十进制计数。

位权： 可以借助于十进制计数来理解位权，在十进制计数中，计数单位分别为个位、十位、百位……，其中个位数表示数值1、十位数表示数值10、百位数表示数值100…每个位数表示的数值叫位权。位权通过计算基数的n-1次幂就可以得到，这里的n是指位数所在数字中的位置

E.g.：二进制数00111从低位到高位的位权依次是2的0次幂1、2的1次幂2、2的2次幂4···

按位与(&)：
按位与（bitwise AND） 操作是一种基于二进制的运算，会逐位比较两个数的二进制位，并根据以下规则生成一个新值：
如果两个位都为 1，结果为 1；
 如果任意一位为 0，结果为 0。 例子： 假设我们有两个数字：

  • 6 的二进制表示是 0110

  • 3 的二进制表示是 0011 6 & 3 的按位与结果为：
    0110 （6）
    0011 （3）
    0010 （结果 = 2）

通常作用
1. 按位与可以用于清除特定位，即将某些位强制设置为 0，而不影响其他位。
例如：
x = 1011 1011 (即十进制的187)

mask = 1111 0000 (掩码，将低 4 位清零)

结果 = 1011 0000 (即十进制的176)

(2) 检查特定位是否为 1 :

例如，检查某数的第三位是否为 1：
x = 0110 (即 6)
mask = 0100 (掩码，检查第三位)
结果 = 0100 (非零，表示第三位为 1)

快速幂取模

一个折腾了笔者好久的算法，书本看了好几遍没看懂，所以到处寻找是不是由于二进制没学透，后来发现是数学没学好😭😭😭😭😭 一定要学好数学
所以，快速幂取模算法只需要在快速幂算法的基础上在特定地方加取模就OK 

int modexp(int a,int b,int n){
    int ans = 1,res = a;
    while(b>0){
        if(i%2==1){//当然可以用i & 1
            ans=(ans*res)%n;
        }
        i/=2;//当然也可以用i >> 2
        res=(res*res)%n;
    }
    return ans;
}
沟槽的玩意，看了我半天，怎么会有书把原理写在下一页

时间复杂度：O( \(\log_2 n\) )
附一张基本模运算的表

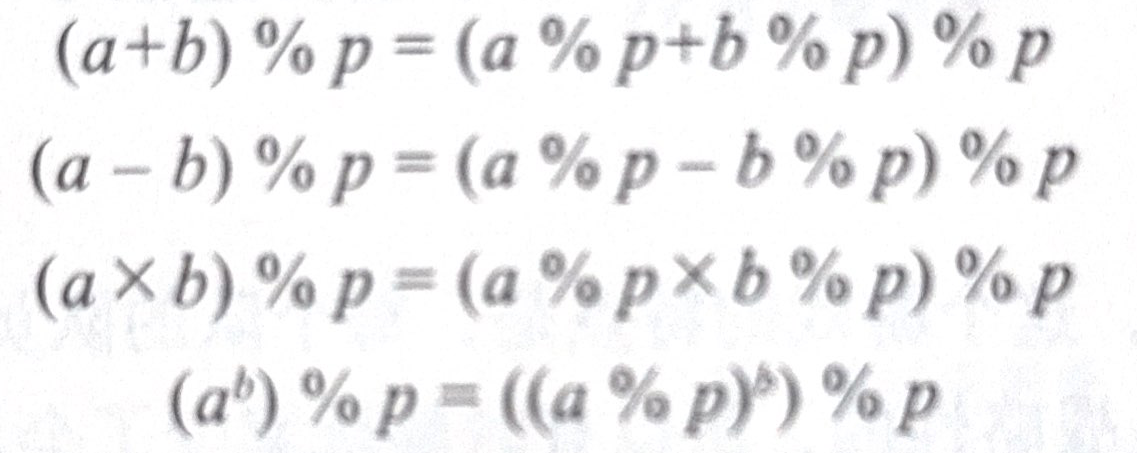
矩阵快速幂

矩阵快速幂的原理其实和普通快速幂一模一样，唯一的区别就是把相乘的对象从数字/字母变成了一坨矩阵，相乘的方式也是从直接✖️变成了复杂的矩阵乘法
矩阵乘法的原理这里笔者就不加赘述，上代码！

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;

int M,n;

struct node//定义一个矩阵类型的结构体
{
    int m[100][100];
} ans,res;//ans是结果，res是最初的方阵
node mul(node A,node B)
{
    int i,j,k;
    node temp;//定义一个临时矩阵，存放A*B的结果
    for(i=0; i<n; i++)//先全部定义为0
    {
        for(j=0; j<n; j++)
        {
            temp.m[i][j] = 0;
        }
    }
    for(i=0; i<n; i++)//矩阵相乘的代码
    {
        for(j=0; j<n; j++)
        {
            for(k=0; k<n; k++)
            {
                temp.m[i][j] += A.m[i][k] * B.m[k][j];
            }
        }
    }
    return temp;
}


void quickpower(int M,int n){
    int i,j;
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            if(i == j) ans.m[i][j] = 1;
            else       ans.m[i][j] = 0;
        }
    }//这里是思想的转换，之前我们定义为1去计算，所以我们先初始化ans为单位矩阵（单位矩阵的定义就是除了主对角线是1，其他位置全都是0，这样子乘上任何一个矩阵都会等于本身）
    while(M)//快速幂的步骤
    {
        if(M & 1)//就是M%2==1
            ans = mul(ans,res);
        res = mul(res,res);
        M = M >> 1;
    }
}
int main()
{
    cin>>n;//方阵的阶数
    cin>>M;//指数
    int i,j;
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            cin>>res.m[i][j];//初始化方阵res
        }
    }
    quickpower(M,n);//进行快速幂
    for(i=0; i<n; i++)//输出
    {
        for(j=0; j<n; j++)
        {
            printf("%d ",ans.m[i][j]);
        }
        printf("\n");
    }
    return 0;
}

矩阵快速幂的直接运用：计算斐波那契数列

#include <stdio.h>
const int MOD = 10000;
struct matrix{
    int m[2][2];
}ans;//定义结构体矩阵
matrix base={1,1,1,0}//数列首项
matrix multi(matrix a,matrix b){
    matrix tmp;
    for(int i=0,i<2;i++){
        for(int j=0;j<2;j++){
            tmp.m[i][j]=0;
            for(int k=0;k<2;k++){
                tmp.m[i][j]=(tmp.m[i][j]+a.m[i][k]*b.m[k][j];) % MOD;
            }
        }
    }
    return tmp;
}
int matrix_pow(matrix a,int n){
    ans.m[0][0]=ans.m[1][1]=1;
    ans.m[0][1]=ans.m[1][0]=0;
    while(n){
        if(n & 1){
            ans=multi(ans,a);
        }
        a=multi(a,a);
        n>>=1;

    }
    return ans.m[0][1];
}
int main(){
    int n;
    //输入输出就不写了；
}